Using Artificial Intelligence to Enhance Mathematics Resources: Checks for understanding
I will share some ideas on how I have found AI can support in checks for understanding in the secondary Mathematics classroom.
In my previous post (linked below), I shared ideas on how Artificial Intelligence can help create sets of questions tailored to students in your classroom, aiming to aid student learning and reduce teacher workload. I want to continue this by suggesting how AI might help with checks for understanding, again tailored for the students in your classroom, in a time-efficient way.
Key points
As before, I’m using Gemini to create everything. The way I am generating and displaying this is the same as before, as explained in my previous post. The post also includes fixes for common errors or problems you may encounter.
I am using mini-whiteboards alongside these generated resources to gather student feedback. As a side note, although these resources are being made in advance of the lesson, by nature of these being checks for understanding, if you need to adapt what you are doing during your lesson in response to the feedback you are seeing from students, you should.
Checks for understanding
When I refer to ‘checks for understanding’, I am checking if students can perform what I need them to at this point in the lesson. For the learning to be sustained, retrieval will inevitably be essential. The idea of using multiple-choice questions and receiving whole-class feedback from mini-whiteboards is, I think, fairly commonplace in classrooms, so I won’t focus on how this works; instead, I'll focus on the questions to ask.
I usually aim to ask questions with 4 multiple-choice answers, with the wrong answers, where possible, arising from common misconceptions or common procedural errors. Below is an example of one such question that I have previously written for a lesson:
I have also previously used the fantastic bank of questions on “Diagnostic Questions” (https://diagnosticquestions.com/); however, I often found myself spending a long time looking for suitable questions for my particular lesson and class, with varying levels of success. I have spent time writing my own questions, which works as a solution, but it is time-consuming, especially when I am thinking of common misconceptions/errors to include in the options for solutions.
Using Artificial Intelligence to Write the Questions
There are two situations where I’ve found AI helpful: one is when I want a sequence of questions that progress in difficulty and flow well, and that also checks for misconceptions (Scenario 1). The other is when breaking down processes into individual component parts, where generating checks for understanding yourself would be very time-consuming, and these questions generally won’t already exist to find and use (Scenario 2).
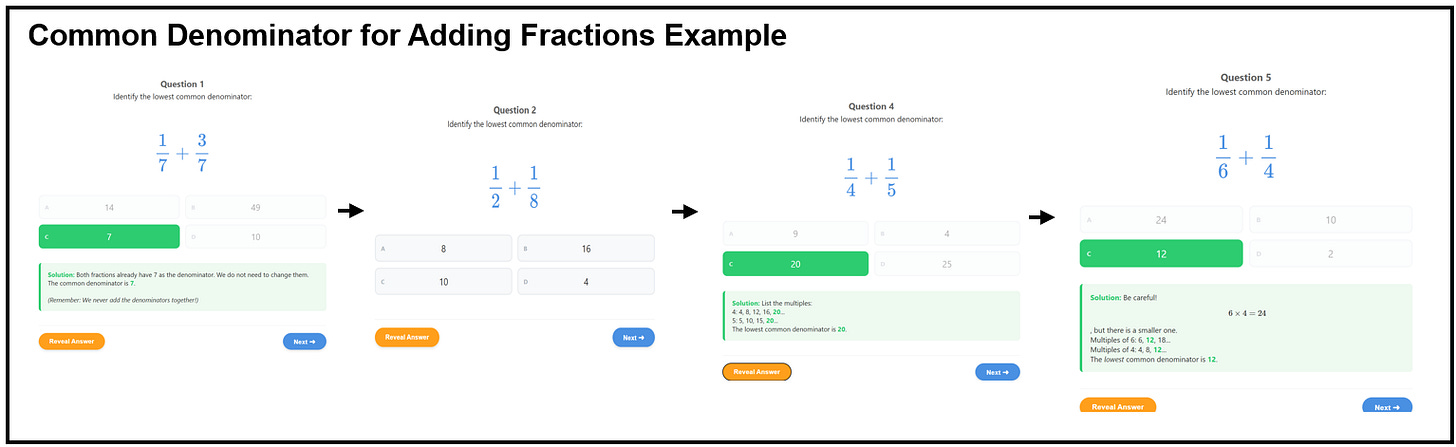
Scenario 1: Below is a set of questions I have asked Gemini to generate on the process of finding the lowest common denominator before adding fractions.
Notice that the questions progress in difficulty, so they flow well, and that AI can identify and use common student misconceptions. One such example is the misconception that multiplying the denominators always gives the lowest common denominator, which has been explicitly identified and checked for, as seen in question 5. Another example is the common denominator of 16 in question 2, where students do not realise that 8 is the LCM of 2 and 8.
Another example, from a sequence of questions on identifying coefficients in a quadratic equation, is given here:
Again, you will note that Answer A has the common misconception of labelling a,b,c from left to right. Answer C has the misconception of labelling the x coefficient as 0. Answer D has a mix of these. I have also been able to control the sequencing of the questions, for example, ensuring that all terms are positive in the first 3 questions. The exact prompt used to generate this is at the end of this post. The full interactive version of this is available here (note that if opening, this is designed for desktop, not mobiles).
You should, of course, check these questions in advance of the lesson, so that you know which answers relate to which misconceptions or errors.
Scenario 2: I am teaching a low-attaining Year 10 class how to calculate the mean from a frequency table. I have broken down the individual parts of the process into smaller ‘atoms’ while teaching, rather than explaining the whole process at once, because I know I will lose the class if I show the entire process from the start and expect students to follow it all. I want to check for understanding at each point.
We are looking at the following frequency table:
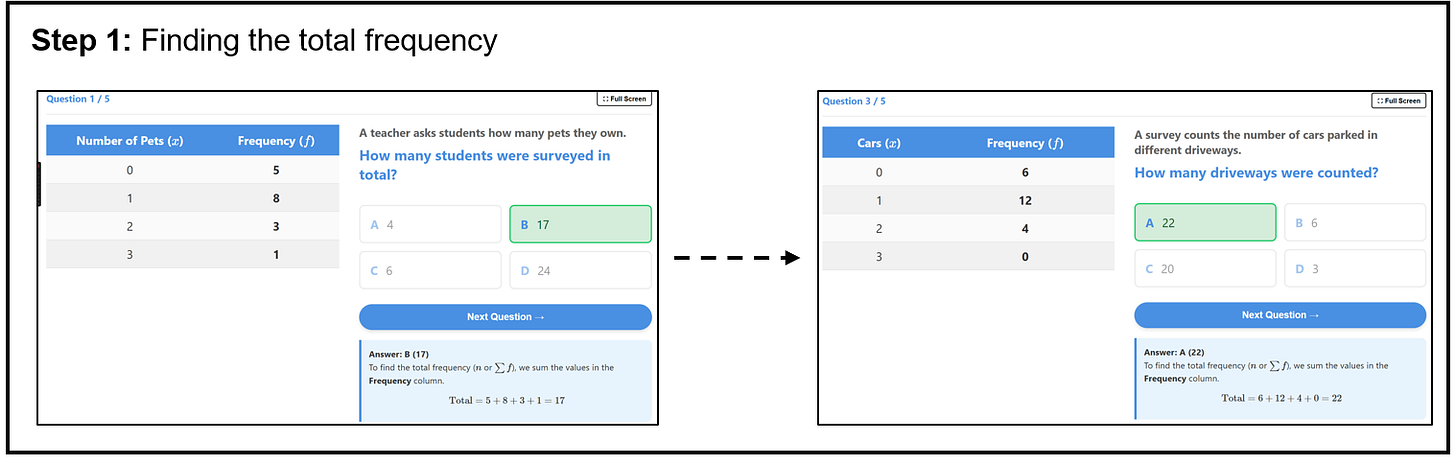
I want students first to understand that the total frequency represents the number of students who took the quiz, and to get used to finding the total frequency as part of the process for finding the mean. I model this (in various scenarios), then I want to check for understanding.
I ask Gemini to generate a set of 5 questions that check this, two of which can be seen here:
You could, of course, specify if you do not want to use the sigma notation; however, I am happy with this for my class. Note that you could, at this point, also generate a set of independent practice questions on this, using the process described in my previous post.
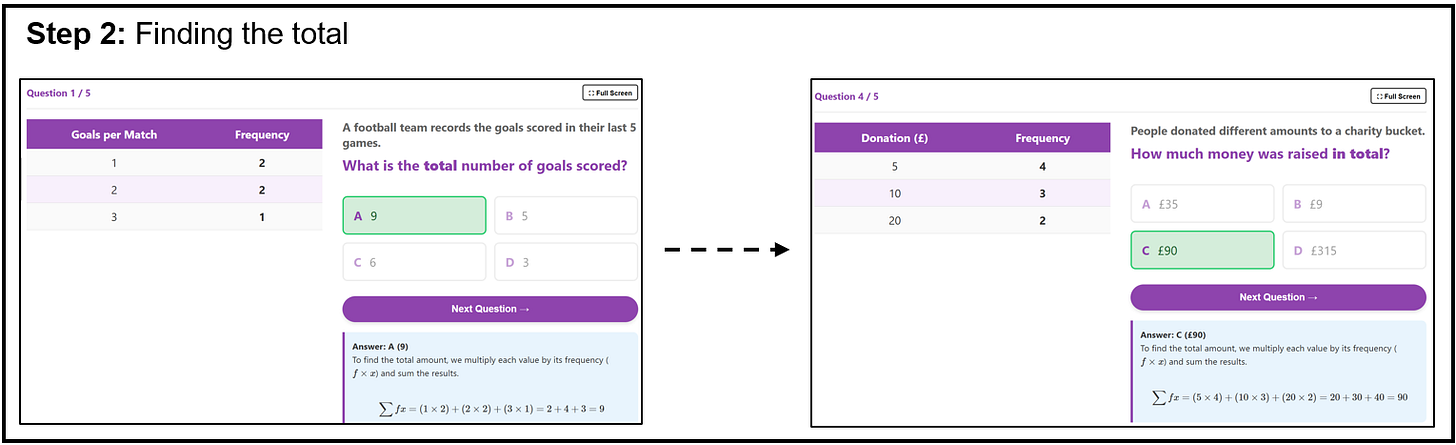
Once I am confident that students are comfortable with this, I move on to the next step: calculating the total in each table.
Again, I want students to focus on one particular step, so after modelling this, I generate a set of questions to check for understanding, as seen below:
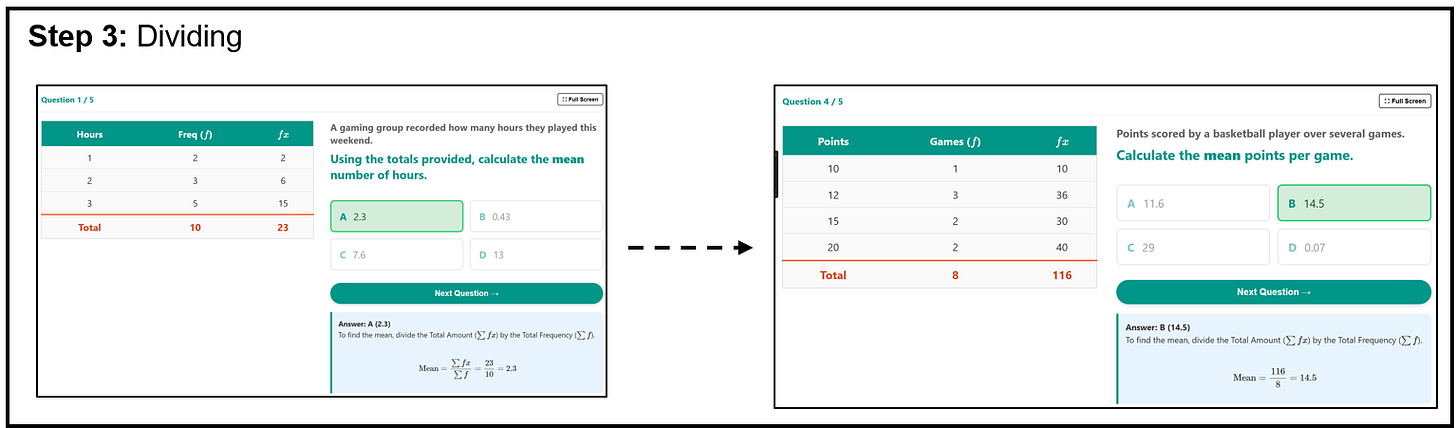
The final step, dividing the totals (in the original example: 153 ÷ 20), can also be practised in isolation, after appropriate modelling. I again generate a set of questions focusing on this:
(Notice again, it includes an answer that arises from a very common misconception: 23 ÷ 3 = 7.666 in question 1).
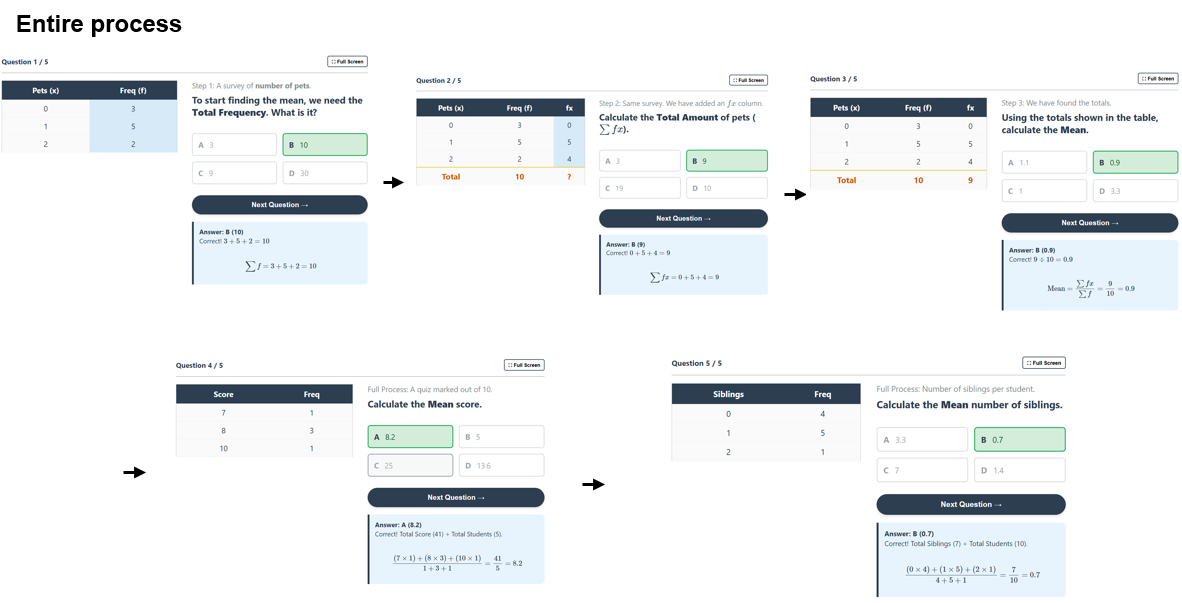
The final step is to bring this together into one process, and again check for understanding. I’ve asked for the first 3 questions to piece it together, then the final 2 for students to complete the entire process themselves.
This aims to illustrate one way in which using AI has allowed me to capture detailed checks for understanding throughout the lesson, without taking up masses of time to produce the questions.
Conclusion & The Prompts
Below, I’ll share the prompts I put into Gemini to yield the results shown above. You can change any parts of the prompt to be more specific or make improvements. The more specific you are, the better results you will get.
As before, I hope that if you’ve read this far, you might be inspired to do something similar (or better!) to aid student understanding and reduce your own workload.
The prompt I use as the ‘set up’
You are an expert maths teacher and resource creator. You use pedagogy and methodology that is known to improve student outcomes when you create resources. Your task will be to create an activity designed as a mini-whiteboard check for understanding, using HTML, CSS, MathJax for Maths formatting, and any other suitable libraries for diagrams and graphs. Questions should be one per page, with multiple choice answers, each labelled as A,B,C,D.
Wrong answers should be answers that arise from common misconceptions or procedural errors, where possible. Questions should gradually increase in difficulty as they progress. I should be able to click “Reveal answer” for each question, the correct answer should turn green, along with a worked solution or explanation below to support student understanding. I should be able to click “Next” to navigate between questions. Include a button to make it full screen. It should look modern, colourful, simple. Ensure the question and worked solutions when revealed all put on one standard size laptop screen. Also ensure that scrolloing is enabled. Check there are no formatting errors in the code you have produced. The specific questions
Next, you will need to describe in detail the questions you’d like. One example prompt is given below.
Generate a set of 5 questions which are suitable for finding the mean from a frequency table, ungrouped data. The questions should be focused on one specific step, which is finding the total frequency. The questions asked should be in context e.g. "How many students took the quiz". This activity is designed to support student understanding in what total frequency represents and to give students practice in this step of the full process.Another prompt:
Create a set of 6 questions for a middle attaining year 11 class on identifying the a, b, c values of a quadratic expression before using the quadratic formula. In the first 3 questions, all terms should be positive, with the order of the terms changing. The next 3 should include negative terms, and again, move the order of the terms around.The provided interactive activity from these exact prompts is here: Click here
To display the generated code, follow the steps outlined in my previous post.
Thanks for reading. I hope you can take something away from this!